5 Juegos MatemáTICos para desarrollar la lógica matemática.
Belén Mariño
@blntab
Lógica y matemáticas para todos
INTRODUCCIÓN
Los juegos de lógica y razonamiento siempre han causado sensación entre el público de cualquier edad. Son propuestas lúdicas, motivadoras y curiosas, y una forma distinta de ver las matemáticas.
Una de las razones más importantes que avalan el aprendizaje de las matemáticas es su trascendencia en otras disciplinas como la física, la ingeniería, la medicina, la informática, etc.
Los matemáticos justifican el aprendizaje y comprensión de los contenidos de esta área atribuyéndole unas cualidades especiales: estimular la capacidad de razonamiento, las facultades para el pensamiento lógico, la visión espacial, etc. Sin embargo, también debemos tener en cuenta otros aspectos: las matemáticas nos ayudarán a hacer frente a determinados problemas cotidianos, son un instrumento fundamental para presentar la información de diversas formas (números, diagramas, dibujos geométricos...).
Pero está claro que es necesario reivindicar y estimular el gusto por las matemáticas.
Es importante proponer a niñas y niños problemas de ingenio, juegos mágicos que estimularán el aprendizaje por las matemáticas y conseguirán una mejor comprensión de las mismas.
OBJETIVOS
Está formado por:
Si queremos, podemos descargarlo, pegarlo en goma eva o cartulina y jugar con él.

4. Cuadrado oculto
5. Enigmas, acertijos y problemas de ingenio
La curiosa tendencia de proponer y resolver enigmas es innata en las personas. Nos enfrentamos a la necesidad constante de solucionar problemas. Dar respuesta a un enigma, acertijo o problema supone poner en acción nuestro ingenio y nuestra habilidad, que se sirven de las matemáticas, esa ciencia tan incomprendida para muchos, y de la lógica.
Al igual que sucede con el deporte, el ejercicio mental diario produce resultados beneficiosos para nuestra mente. Los acertijos mantienen la mente clara, estimulan la imaginación y desarrollan la facultad de razonamiento. Y no solo nos resultan útiles en esta forma indirecta, sino que en muchas ocasiones nos ayudan enseñándonos pequeños trucos y estrategias que podemos aplicar a la vida cotidiana.
¿Te atreves con este problema?
"En un colegio se celebró un torneo entre los equipos A, B, C y D. El equipo ganador conseguía dosp untos; los que empataban, un punto cada uno, y los que perdían, ninguno. Lo curioso es que cada uno de los equipos metió un gol, y aun así la clasificación fue:
A = 4 puntos
B = 4 puntos
C = 3 puntos
D = 1 punto
¿Cuáles fueron los resultados de los partidos?"
RECURSOS:
Haiku Deck
BIBLIOGRAFÍA
Los matemáticos justifican el aprendizaje y comprensión de los contenidos de esta área atribuyéndole unas cualidades especiales: estimular la capacidad de razonamiento, las facultades para el pensamiento lógico, la visión espacial, etc. Sin embargo, también debemos tener en cuenta otros aspectos: las matemáticas nos ayudarán a hacer frente a determinados problemas cotidianos, son un instrumento fundamental para presentar la información de diversas formas (números, diagramas, dibujos geométricos...).
Pero está claro que es necesario reivindicar y estimular el gusto por las matemáticas.
Es importante proponer a niñas y niños problemas de ingenio, juegos mágicos que estimularán el aprendizaje por las matemáticas y conseguirán una mejor comprensión de las mismas.
OBJETIVOS
- Resolver problemas geométricos utilizando estrategias de razonamiento, creando conjeturas, argumentando y tomando decisiones.
- Identificar e interpretar datos y textos numéricos.
- Utilizar las propiedades de las figuras planas para resolver problemas.
- Interpretar representaciones espaciales realizadas a partir de sistemas de referencia.
- Describir y analizar situaciones de cambio para encontrar patrones, regularidades y leyes matemáticas, en contextos numéricos, geométricos y funcionales, valorando su utilidad para hacer predicciones.
1. Pentaminós
Existen doce pentaminós posibles:
PENTAMINÓS - Created with Haiku Deck, presentation software that inspires
2. Tangram
 Son muchas las teorías y leyendas que se pueden encontrar sobre el origen del Tangram (juego individual que estimula la creatividad).
Son muchas las teorías y leyendas que se pueden encontrar sobre el origen del Tangram (juego individual que estimula la creatividad).
Se trata de un rompecabezas chino denominado "Chi Chiao Pan" o "tabla de la sabiduría".
Ni siquiera la denominación de Tangram tiene un origen muy claro. Una teoría la relaciona con un inglés que la compuso a partir del vocablo cantonés tang y de la palabra latina gram. Otra leyenda sitúa su origen en la época de la dinastía Tang.
Muchas personas de las ciencias, del arte y de muy diversos ámbitos se vieron atraídos por este singular y desafiante rompecabezas. Por ejemplo, Napoleón Bonaparte se volvió un verdadero especialista en el Tangram desde que había sido exiliado a la isla de Santa Elena.
Las piezas, llamadas "Tans", son:
Existen doce pentaminós posibles:
PENTAMINÓS - Created with Haiku Deck, presentation software that inspires
 Son muchas las teorías y leyendas que se pueden encontrar sobre el origen del Tangram (juego individual que estimula la creatividad).
Son muchas las teorías y leyendas que se pueden encontrar sobre el origen del Tangram (juego individual que estimula la creatividad).Se trata de un rompecabezas chino denominado "Chi Chiao Pan" o "tabla de la sabiduría".
Ni siquiera la denominación de Tangram tiene un origen muy claro. Una teoría la relaciona con un inglés que la compuso a partir del vocablo cantonés tang y de la palabra latina gram. Otra leyenda sitúa su origen en la época de la dinastía Tang.
Muchas personas de las ciencias, del arte y de muy diversos ámbitos se vieron atraídos por este singular y desafiante rompecabezas. Por ejemplo, Napoleón Bonaparte se volvió un verdadero especialista en el Tangram desde que había sido exiliado a la isla de Santa Elena.
Las piezas, llamadas "Tans", son:
- 5 triángulos, dos construidos con la diagonal del cuadrado inicial.
- 1 cuadrado.
- 1 paralelogramo o romboide.
También a partir de un cuadrado, vamos dibujando sobre su superficie hasta construirlo:
- Trazamos una diagonal en el cuadrado y una recta que une los puntos medios de dos lados consecutivos, de manera que esta recta sea paralela a la diagonal.
- Trazamos la otra diagonal desde el otro vértice hasta la recta que une los puntos medios.
- Dividimos la primera diagonal en cuatro partes iguales y unimos la primera marca con el punto de intersección entre la segunda diagonal y la recta que unía los puntos medios.
- Trazamos la última recta uniendo la tercera de las marcas de la diagonal con el punto medio dellado del cuadrado.
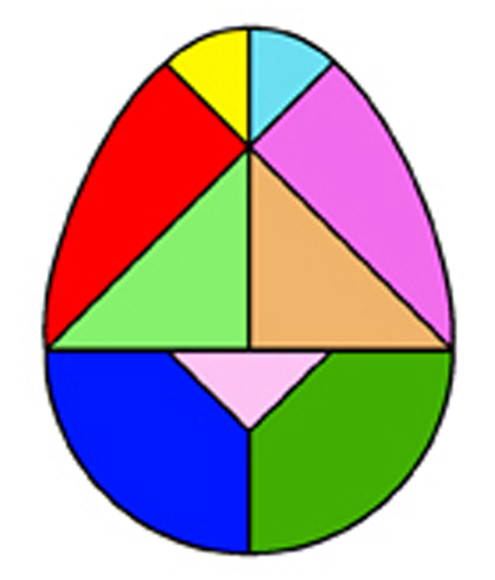
3. Tangram de huevo
Dentro de las variedades de rompecabezas del Tangram, llaman la atención aquellas formadas por piezas curvilíneas ya que lso resultados ganan en matices y los contornos son más suaves.
Entre este tipo podemos encontrar el Cardiotangram, con forma de corazón; Tangram circular y el Tangram de huevo, o Huevo de Colón.
Las nueve piezas que forman el Tangram guardan entre sí unas relaciones geométricas muy especiales y precisas porque nacen todas de un óvalo.
Está formado por:
- dos triángulos isósceles curvos,
- dos triángulos rectángulos curvos,
- dos triángulos rectángulos grandes,
- un triángulo rectángulo pequeño,
- dos trapecios curvos.
- Dibuja en círculo de radio 6 cm. y marca el centro con una A.
- Traza los diámetros BC y DE, de forma que determinen un ángulo recto.
- Une B a E y E a C y luego alarga estas dos líneas 5 cm. por encima de E.
- Utilizando B como centro y BC como radio, traza un arco que corte la prolongación de la línea BE en G.
- Utilizando C como centro y CB como radio, traza un arco que corte la prolongación de la línea CE en F.
- Con E como centro y EF como radio, traza un arco que una F y G.
- Mide este mismo radio desde D a lo largo de la línea DA para determinar el punto H.
- Con ese mismo radio y H como centro, traza un arco que cruce la línea BC en J y en K.
- Alarga la línea AE hasta que corte el arco FG en L.
- Une H con J y después H con K.
Su invención está fechada en Alemania, a finales de la década de los noventa del siglo XIX, por los hermanos Otto y GustavLilienthal ingenieros y pioneros de la aviación inventaron una forma de reproducir unos bloques de manera manuales, llamados piedras de Anker, a partir de arena de cuarzo, yeso y aceite de linaza.
La patente de estos bloques fue adquirida posteriormente por Fiedrich A. Richter, quien a partir de 1890 lanzó una línea de puzzles hechos con piedras Anker que podían combinarse para formar figuras nuevas. Uno de ellos fue el Tangram ovalado, que vio la luz en 1893, y en el cual se proponían la formación de 95 figuras diferentes con las nueve piezas componentes.
Si queremos, podemos descargarlo, pegarlo en goma eva o cartulina y jugar con él.


4. Cuadrado oculto
- A partir de cierto número de piezas, un puzzle puede dar lugar a múltiples figuras geométricas.
- Si dibujamos un triángulo o un cuadrado y lo cortamos en piezas de líneas rectas, podríamos componer un hexágono.
- El truco consiste en cortar la figura original en el menor número de piezas.
5. Enigmas, acertijos y problemas de ingenio
La curiosa tendencia de proponer y resolver enigmas es innata en las personas. Nos enfrentamos a la necesidad constante de solucionar problemas. Dar respuesta a un enigma, acertijo o problema supone poner en acción nuestro ingenio y nuestra habilidad, que se sirven de las matemáticas, esa ciencia tan incomprendida para muchos, y de la lógica.
Al igual que sucede con el deporte, el ejercicio mental diario produce resultados beneficiosos para nuestra mente. Los acertijos mantienen la mente clara, estimulan la imaginación y desarrollan la facultad de razonamiento. Y no solo nos resultan útiles en esta forma indirecta, sino que en muchas ocasiones nos ayudan enseñándonos pequeños trucos y estrategias que podemos aplicar a la vida cotidiana.
¿Te atreves con este problema?
"En un colegio se celebró un torneo entre los equipos A, B, C y D. El equipo ganador conseguía dosp untos; los que empataban, un punto cada uno, y los que perdían, ninguno. Lo curioso es que cada uno de los equipos metió un gol, y aun así la clasificación fue:
A = 4 puntos
B = 4 puntos
C = 3 puntos
D = 1 punto
¿Cuáles fueron los resultados de los partidos?"
RECURSOS:
Haiku Deck
BIBLIOGRAFÍA
- "Juega y sorpréndete con las matemáticas". Segarra, Luís. Círculo de Lectores.
- "Enigmática. Enigmas y juegos matemáticos". Segarra, Luís. Círculo de Lectores.
- "Juegos para desarrollar la inteligencia, la creatividad y la habilidad manual" Casamento, Enzo. Editorial de Vecchi.
- "Uno + uno son diez". Letona, José Mª. Editorial La Muralla.


























.JPG)


1 comentarios
Genial!!!!!! Muy buen trabajo!!!
ResponderEliminarPuedes dejar tu comentario, formulando preguntas, solicitando nuevos enlaces, ampliando información o sugiriendo mejoras. Seguro que tienes algo que decirnos...